कक्षा 12 भौतिकी के लिए एनसीईआरटी समाधान अध्याय 1 विद्युत प्रभार और क्षेत्र कक्षा 12 भौतिकी के लिए एनसीईआरटी समाधान का हिस्सा हैं । यहां हमने दिया है। कक्षा 12 भौतिकी के लिए एनसीईआरटी समाधान अध्याय 1 विद्युत आवेश और क्षेत्र
NCERT Solutions For Class 12 Physics Chapter 1 Electric Charges And Fields
| तख़्ता | सीबीएसई |
| पाठयपुस्तक | NCERT |
| कक्षा | कक्षा 12 |
| विषय | भौतिक विज्ञान |
| अध्याय | अध्याय 1 |
| अध्याय का नाम | विद्युत प्रभार और क्षेत्र |
| हल किए गए प्रश्नों की संख्या | 34 |
| श्रेणी | NCERT Solutions |
प्रश्न 1. हवा में 30 सेंटीमीटर की दूरी पर रखे
2 x 10 -7 C और 3 x 10 -7 Cआवेश वाले दो छोटे आवेशित गोलों के बीच लगने वाला बल क्या है?
उत्तर:
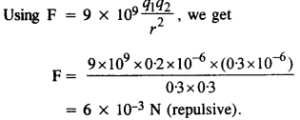
प्रश्न 2.
0.4 μC आवेश के एक छोटे से गोले पर -0.8 μC आवेश के एक अन्य छोटे गोले के कारण इलेक्ट्रोस्टैटिक बल 0.2 N है।
(a) दो क्षेत्रों के बीच की दूरी क्या है?
(ख) पहले गोले के कारण दूसरे गोले पर कितना बल है?
उत्तर:
(ए) चार्ज 2 के कारण चार्ज 1 पर बल संबंध द्वारा दिया गया है
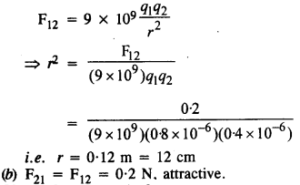
प्रश्न 3.
जाँच कीजिए कि अनुपात ke 2 / G m e m p है । आयामहीन है। भौतिक स्थिरांक की एक तालिका देखें और इस अनुपात का मान निर्धारित करें। अनुपात क्या दर्शाता है?
उत्तर:
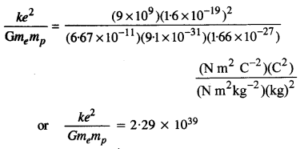
इस प्रकार, दिया गया अनुपात एक संख्या है और विमाहीन है। यह अनुपात दर्शाता है कि इलेक्ट्रॉन और प्रोटॉन के बीच इलेक्ट्रोस्टैटिक बल उनके बीच गुरुत्वाकर्षण बल की तुलना में बहुत अधिक है।
प्रश्न 4.
(a) ‘किसी पिंड का विद्युत आवेश परिमाणित है’ कथन का अर्थ स्पष्ट कीजिए।
(बी) मैक्रोस्कोपिक यानी बड़े पैमाने पर चार्ज से निपटने के दौरान कोई इलेक्ट्रिक चार्ज की मात्राकरण की उपेक्षा क्यों कर सकता है?
उत्तर:
(ए) एक असतत इकाई के रूप में प्रकृति में चार्ज होता है। चार्ज के एक पैकेट (न्यूनतम मात्रा) को क्वांटम चार्ज कहा जाता है। इसे ‘ई’ द्वारा दर्शाया जाता है। आम तौर पर, इलेक्ट्रॉन का चार्ज ‘ई’ द्वारा दर्शाया जाता है और प्रोटॉन का चार्ज ‘+ ई’ द्वारा दर्शाया जाता है। इसलिए, किसी भी आवेशित पिंड का आवेश ± e का एक अभिन्न गुणज होगा, अर्थात, ne जहाँ n = 1, 2, 3,
q = ± ne
तथ्य यह है कि विद्युत आवेश संग्रह मौलिक इलेक्ट्रॉनिक आवेश के अभिन्न गुणज हैं मिलिकन द्वारा प्रयोगात्मक रूप से सिद्ध किया गया था।
(बी) बड़े पैमाने पर विद्युत घटना से निपटने के दौरान, हम आवेश के परिमाणीकरण की उपेक्षा करते हैं क्योंकि प्रोटॉन और इलेक्ट्रॉन के आवेश का परिमाण इतना छोटा होता है। निरंतर चार्ज वितरण के लिए, चार्ज को चार्ज डेंसिटी जैसे लीनियर चार्ज डेंसिटी λ आदि के रूप में हिसाब किया जा सकता है। हमें अलग-अलग चार्ज के लिए जाने की जरूरत नहीं है।
प्रश्न 5.
कांच की छड़ को रेशमी कपड़े से रगड़ने पर दोनों पर आवेश दिखाई देते हैं। इसी तरह की घटना कई अन्य जोड़े निकायों के साथ देखी जाती है। स्पष्ट कीजिए कि यह प्रेक्षण किस प्रकार आवेश संरक्षण के नियम के अनुरूप है।
उत्तर:
रगड़ने से पहले, कांच की छड़ और रेशमी कपड़े दोनों विद्युत रूप से तटस्थ होते हैं। दूसरे शब्दों में, कांच की छड़ और रेशमी कपड़े पर शुद्ध आवेश शून्य होता है। जब कांच की छड़ को रेशमी कपड़े से रगड़ा जाता है, तो कांच की छड़ से कुछ इलेक्ट्रॉन रेशमी कपड़े में स्थानांतरित हो जाते हैं। नतीजतन, कांच की छड़ सकारात्मक रूप से चार्ज हो जाती है और रेशमी कपड़ा नकारात्मक रूप से चार्ज हो जाता है। चूँकि कांच की छड़ पर धनात्मक आवेश का परिमाण रेशम पर ऋणात्मक आवेश के समान होता है, इसलिए निकाय पर शुद्ध आवेश शून्य होता है। इस प्रकार कांच की छड़ और रेशमी कपड़े पर आवेश का दिखना आवेशों के संरक्षण के नियम के अनुसार होता है।
प्रश्न 6.
चार-बिंदु आवेश q A = 2 μC, q B = -5 μC, या q c = -2 μC और q D = -5 μC 10 सेमी भुजा वाले वर्ग ABCD के कोनों पर स्थित हैं। वर्ग के केंद्र में रखे 1μC आवेश पर कितना बल है?
उत्तर:
आकृति की समरूपता स्पष्ट रूप से इंगित करती है कि A और C पर रखे गए 2μC के समान आवेशों के कारण 1μC आवेश समान और विपरीत बलों का अनुभव करेगा। इसी प्रकार, D पर रखे -5 μC आवेशों के कारण 1μC आवेश समान और विपरीत बलों का अनुभव करेगा। B.
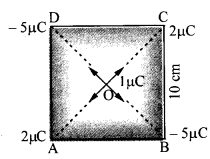
अत: शुद्ध बल = शून्य।
प्रश्न 7.
(a) स्थिरवैद्युत क्षेत्र रेखा एक सतत वक्र है।
अर्थात् किसी क्षेत्र रेखा में अचानक विराम नहीं हो सकता। क्यों नहीं?
(b) स्पष्ट कीजिए कि दो क्षेत्र रेखाएँ कभी भी एक दूसरे को किसी बिंदु पर क्यों नहीं काटती हैं?
उत्तर:
(ए) विद्युत क्षेत्र के पूरे क्षेत्र में बल की विद्युत रेखाएं मौजूद हैं। एक आवेश का विद्युत क्षेत्र उससे बढ़ती दूरी के साथ धीरे-धीरे कम होता जाता है और अनंत पर शून्य हो जाता है (i) e., विद्युत क्षेत्र अचानक गायब नहीं हो सकता है। तो बल की एक रेखा में अचानक विराम नहीं हो सकता है, यह एक निरंतर वक्र होना चाहिए।
(बी) यदि बल की दो रेखाएं प्रतिच्छेद करती हैं, तो दो स्पर्शरेखाएं होंगी और इसलिए चौराहे के बिंदु पर विद्युत क्षेत्र की दो दिशाएं होंगी, जो संभव नहीं है।
प्रश्न 8.
दो-बिंदु आवेश q A = 3μC और q B = -3 μC निर्वात में 20 सेमी की दूरी पर स्थित हैं।
(ए) दो आवेशों को मिलाने वाली रेखा AB के मध्य बिंदु O पर विद्युत क्षेत्र क्या है?
(बी) यदिइस बिंदु पर१.५ x १०- ९ सीपरिमाण का एक ऋणात्मक परीक्षण आवेशरखा जाता है, तो परीक्षण आवेश द्वारा अनुभव किया जाने वाला बल क्या है? (सीबीएसई 2003)
उत्तर:
(ए) दो बराबर और विपरीत चार्ज के बीच अलगाव के मध्य बिंदु पर विद्युत क्षेत्र द्वारा दिया जाता है
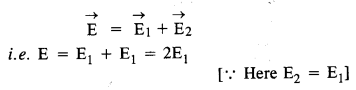
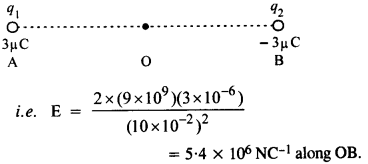
(बी) टेस्ट चार्ज द्वारा अनुभव किया गया बल = क्यू 0 ई
= (1.5 x 10 -9 ) (5.4 x 10 6 )
= 8.1 x 10 -3 एन बीए के साथ
प्रश्न 9.
एक प्रणाली में दो आवेश होते हैं q A = 2.5 x 10 -7 C और q B = -2.5 x 10 -7 C बिंदु
A: (0,0, -15 सेमी) और B: (0, 0, पर स्थित) + 15 सेमी), क्रमशः। निकाय के कुल आवेश और विद्युत द्विध्रुव आघूर्ण क्या हैं?
उत्तर
स्पष्ट रूप से दिए गए बिंदु z-अक्ष पर स्थित हैं।
आवेशों के बीच की दूरी, 21
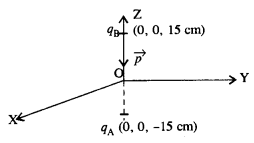
= 15 + 15 = 30 सेमी = 0.3 मीटर
कुल आवेश = (2.5 x 10- 7 ) – (2.5 x 10- 7 ) = 0
द्विध्रुवीय क्षण
= qx 21 = 2.5 x 10- 7 x 0.3
= 7.5 x 10 -8 C m ऋणात्मक z-अक्ष के अनुदिश।
प्रश्न 10.
एक विद्युत द्विध्रुव जिसका द्विध्रुव आघूर्ण 4 x 10 -9 सेमी है, 30° पर 5 x 10 4 NC- 1 परिमाण के एकसमान विद्युत क्षेत्र की दिशा के साथ संरेखित है। द्विध्रुव पर लगने वाले बलाघूर्ण के परिमाण की गणना कीजिए।
उत्तर:
= pE sin 0 का प्रयोग करके, हम प्राप्त करते हैं
= (4 x 10- 9 ) (5x 10- 4 sin 30°)
= 2 x 10- 4 x12= 10- 4 एनएम 2
प्रश्न 11.
एक पॉलिथीन टुकड़ा ऊन के साथ रगड़ने का 3.2 एक्स 10 एक नकारात्मक चार्ज है पाया जाता है 4 सी
(क) (अनुमान इलेक्ट्रॉनों की संख्या का तबादला (जिसमें से करने के लिए जो?)
(ख) वहाँ द्रव्यमान का एक हस्तांतरण है ऊन से पॉलिथीन के लिए?
उत्तर:
(क) का उपयोग करते हुए q = ne पर हम पाते हैं
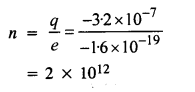
(ख) हाँ, पर नगण्य मात्रा की वजह से एक इलेक्ट्रॉन की बड़े पैमाने पर बहुत-बहुत छोटा है (बड़े पैमाने पर हस्तांतरित = मीटर ई xn = 91 x 10 31 x 2 x 10 12 = 1.82 x 10 -18 किग्रा)।
प्रश्न 12.
(ए) दो अछूता चार्ज तांबे के गोले ए और बी के केंद्र 50 सेमी की दूरी से अलग होते हैं। इलेक्ट्रोस्टैटिक प्रतिकर्षण का पारस्परिक बल क्या है यदि प्रत्येक पर चार्ज 6.5 x 10 – 7 सी है? पृथक्करण की दूरी की तुलना में A और B की त्रिज्याएँ नगण्य हैं।
(बी) यदि प्रत्येक गोले को उपरोक्त राशि से दोगुना चार्ज किया जाता है, और उनके बीच की दूरी आधी कर दी जाती है, तो प्रतिकर्षण बल क्या होता है?
उत्तर:
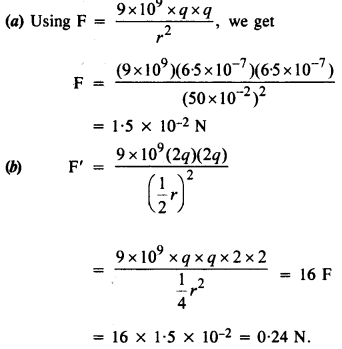
प्रश्न 13.
मान लीजिए कि Q 1.12 में गोले A और B समान आकार के हैं। एक ही आकार का एक तीसरा क्षेत्र लेकिन अपरिवर्तित पहले के संपर्क में लाया जाता है, फिर दूसरे के संपर्क में लाया जाता है, और अंत में दोनों से हटा दिया जाता है। A और B के बीच नया प्रतिकर्षण बल क्या है?
उत्तर:
तीसरे गोले (जैसे C) के संपर्क में आने पर गोले A पर आवेश दिया जाता है, जिसमें कोई आवेश नहीं होता है
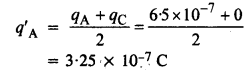
जब तीसरा गोला, 3.25 10 -7 C आवेश वाले गोले को B के संपर्क में कैसे लाया जाता है, तो गोले B पर छोड़ा गया आवेश दिया जाता है द्वारा,
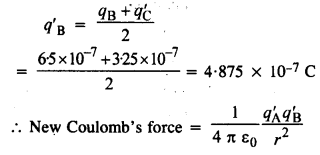
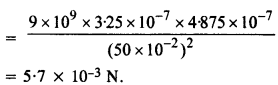
प्रश्न 14.
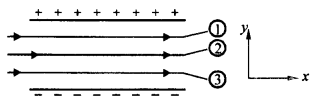
चित्र एकसमान स्थिरवैद्युत क्षेत्र में तीन आवेशित कणों के पथ दिखाता है। तीन आवेशों के लक्षण बताइए। किस कण का आवेश से द्रव्यमान अनुपात सबसे अधिक है?
उत्तर:
विपरीत आवेश एक-दूसरे को आकर्षित करते हैं, इसलिए कण 1 और 2 ऋणात्मक रूप से आवेशित होते हैं जबकि कण 3 में धनात्मक आवेश होता है। कण 3 को अधिकतम विक्षेपण प्राप्त होता है इसलिए इसका उच्चतम आवेश (e) से द्रव्यमान (m) अनुपात होता है क्योंकि विक्षेपण, y α e/m
प्रश्न 15.
एकसमान विद्युत क्षेत्र पर विचार करेंइ→
= ३ x १० ३ मैं^एन / सी।
(ए) 10 सेमी के वर्ग के माध्यम से इस क्षेत्र का प्रवाह क्या है जिसका तल yz तल के समानांतर है?
(बी) उसी वर्ग के माध्यम से प्रवाह क्या है यदि उसके विमान के लिए सामान्य एक्स-अक्ष के साथ 60 डिग्री कोण बनाता है?
उत्तर:
(ए) वर्ग के माध्यम से विद्युत प्रवाह,
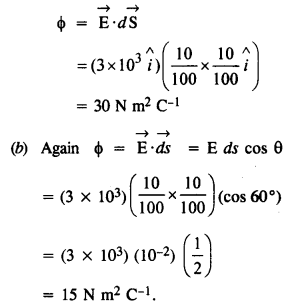
प्रश्न 16.
20 सेमी उन्मुख भुजा के घन के माध्यम से समस्या 1.15 के एकसमान विद्युत क्षेत्र का शुद्ध प्रवाह क्या है ताकि इसके चेहरे समन्वय विमानों के समानांतर हों?
उत्तर
शून्य, क्योंकि घन में प्रवेश करने वाली क्षेत्र रेखाओं की संख्या घन से निकलने वाली क्षेत्र रेखाओं की संख्या के बराबर होती है।
प्रश्न 17.
एक ब्लैक बॉक्स की सतह पर विद्युत क्षेत्र का सावधानीपूर्वक मापन इंगित करता है कि बॉक्स की सतह के माध्यम से नेट आउटवर्ड फ्लक्स 8.0 x 10 3 एनएम2/सी है।
उत्तर:
(ए) बॉक्स के अंदर नेट चार्ज क्या है?
(बी) यदि बॉक्स की सतह के माध्यम से शुद्ध बाहरी प्रवाह शून्य था, तो क्या आप यह निष्कर्ष निकाल सकते हैं कि बॉक्स के अंदर कोई शुल्क नहीं था? क्यों या क्यों नहीं?
उत्तर।
(ए) = φ /ε 0 का उपयोग करके हम प्राप्त करते हैं q =φ 0
= (8 x 10 3 ) (8.854 x 10 -12 )
= 70.8 x 10- 9 C = 0.07 μC
(b)नहीं, ऐसा नहीं कहा जा सकता क्योंकि बॉक्स के अंदर समान संख्या में सकारात्मक और नकारात्मक प्राथमिक परिवर्तन हो सकते हैं। यह केवल इतना ही कहा जा सकता है कि बॉक्स के अंदर का नेट चार्ज शून्य है।
प्रश्न 18.
एक बिंदु आवेश + 10 μC, 10 सेमी भुजा वाले वर्ग के केंद्र से सीधे 5 सेमी की दूरी पर है, जैसा कि चित्र में दिखाया गया है। वर्ग के माध्यम से विद्युत प्रवाह का परिमाण क्या है? [संकेत। वर्ग को 10 सेमी किनारे वाले घन के एक तथ्य के रूप में सोचें।]
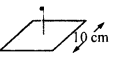
उत्तर:
जैसा कि चित्र में दिखाया गया है, चार्ज को माना जा सकता है।
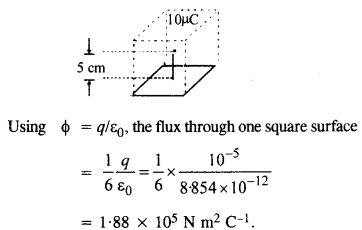
प्रश्न 19.
2.0 μC का एक बिंदु आवेश एक घन गाऊसी सतह के केंद्र में 9.0 सेमी किनारे पर है। सतह के माध्यम से शुद्ध विद्युत प्रवाह क्या है?
उत्तर:
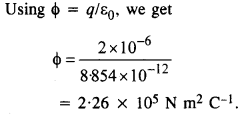
प्रश्न 20.
एक बिंदु आवेश के कारण -1.0 x 10 3 Nm 2 /C काविद्युत प्रवाहआवेश पर केंद्रित 10.0 सेमी त्रिज्या की गोलाकार गॉसियन सतह से होकर गुजरता है।
(ए) यदि गाऊसी सतह की त्रिज्या दोगुनी कर दी जाती है, तो सतह से कितना फ्लक्स गुजरेगा?
(बी) बिंदु प्रभार का मूल्य क्या है?
उत्तर:
(ए) विद्युत प्रवाह केवल गॉसियन सतह से घिरे चार्ज पर निर्भर करता है और गॉसियन सतह के आकार से स्वतंत्र होता है। नई गाऊसी सतह के माध्यम से विद्युत प्रवाह समान रहता है
अर्थात -1 x 10 3 एनएम 2 सी -1 क्योंकि इस मामले में भी संलग्न चार्ज समान रहता है।
(बी)= q/ε 0 का प्रयोग करते हुए , हमें q = ε 0 φ = (8.85 x 10-12 ) (-1 x 10 3 )
अर्थात q = -8.85 x 10 -9 C प्राप्त होता है।
प्रश्न 21.
10 सेमी त्रिज्या वाले एक चालक गोले पर अज्ञात आवेश होता है। यदि गोले के केंद्र से 20 सेमी विद्युत क्षेत्र 1.5 x 10 3 N/C है और रेडियल रूप से अंदर की ओर इंगित करता है, तो गोले पर शुद्ध आवेश क्या है?
उत्तर:
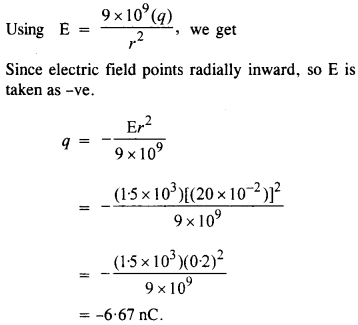
प्रश्न 22.
एक समान रूप से 2.4 मीटर व्यास के क्षेत्र 80.4 μC / मीटर की सतह चार्ज घनत्व का आयोजन किया गया है आरोप लगाया 2 ।
(ए) गोले पर चार्ज का पता लगाएं।
(बी) गोले की सतह को छोड़ने वाला कुल विद्युत प्रवाह क्या है? (बीएसई 2009 सी)
उत्तर:
(ए) गोले पर चार्ज द्वारा दिया जाता है
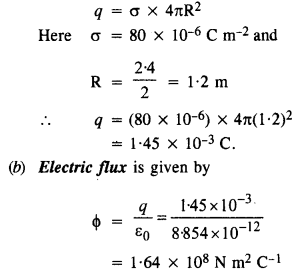
प्रश्न 23.
एक अनंत रेखा आवेश2 सेमी की दूरी पर9 X 10 4 N/Cका क्षेत्र उत्पन्न करता है। रैखिक चार्ज घनत्व की गणना करें
उत्तर:
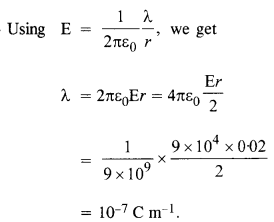
प्रश्न 24.
धातु की दो बड़ी, पतली प्लेटें समानांतर और एक दूसरे के करीब हैं। उनके आंतरिक फलकों पर, प्लेटों में विपरीत संकेतों के सतह आवेश घनत्व और परिमाण 17.0 x 10 -22 C/m 2 होते हैं । ई क्या है?
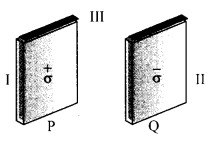
(ए) पहली प्लेट के बाहरी क्षेत्र में,
(बी) दूसरी प्लेट के बाहरी क्षेत्र में, और
(सी) प्लेटों के बीच?
उत्तर:

प्रश्न 25. मिलिकन के तेल बूंद प्रयोग
में 12 अतिरिक्त इलेक्ट्रॉनों की एक तेल बूंद 2.55 x 10 4 एनसी -1 के निरंतर विद्युत क्षेत्र के तहत स्थिर रखी जाती है। तेल का घनत्व 1.26 ग्राम सेमी -3 है । बूंद की त्रिज्या का अनुमान लगाएं, (g = 9.81 ms -2 ; e = 1.60 x 10 -19 C.)
उत्तर:
बूंद पर आवेश,
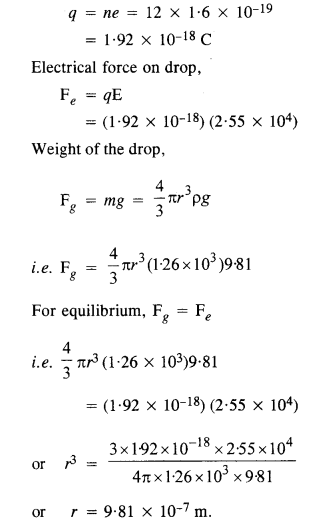
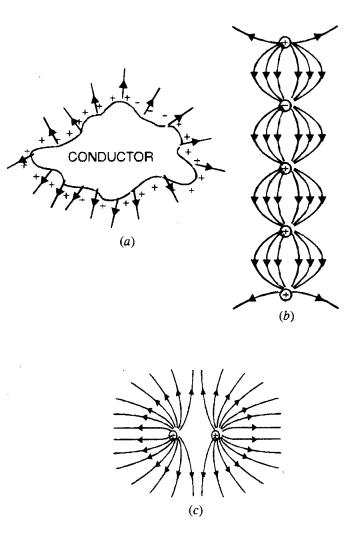
प्रश्न 26.
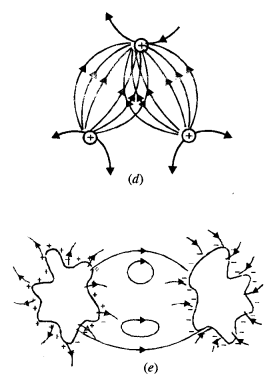
आकृति में दिखाए गए वक्रों में से कौन सा संभवतः इलेक्ट्रोस्टैटिक क्षेत्र रेखाओं का प्रतिनिधित्व नहीं कर सकता है?
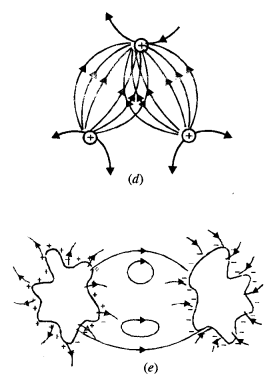
उत्तर:
(ए) गलत, क्योंकि क्षेत्र रेखाएं कंडक्टर की सतह के लिए सामान्य होनी चाहिए।
(बी) गलत, क्योंकि क्षेत्र रेखाएं एक नकारात्मक चार्ज से शुरू नहीं हो सकती हैं।
(सी) सही
(सी) गलत, क्योंकि विद्युत क्षेत्र रेखाएं एक दूसरे के साथ छेड़छाड़ नहीं कर सकती हैं।
(डी) गलत, क्योंकि इलेक्ट्रोस्टैटिक क्षेत्र रेखाएं बंद लूप नहीं बना सकती हैं।
Question 27.
अंतरिक्ष के एक निश्चित क्षेत्र में, विद्युत क्षेत्र z-दिशा के साथ-साथ होता है। हालाँकि, विद्युत क्षेत्र का परिमाण स्थिर नहीं है, लेकिन सकारात्मक z-दिशा के साथ समान रूप से 105NC-1प्रति मीटरकी दर से बढ़ता है। नकारात्मक z-दिशा में10-7C m केबराबर कुल द्विध्रुवीय क्षण वाले सिस्टम द्वारा अनुभव किए गए बल और टोक़ क्या हैं?
उत्तर:
मान लीजिए कि द्विध्रुव z-अक्ष के अनुदिश है।
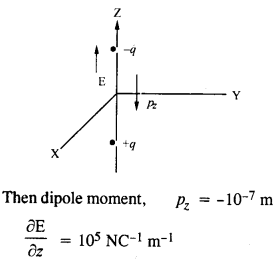
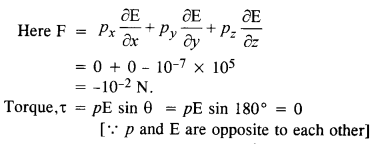
प्रश्न 28.
(ए)एक कंडक्टर ए जिसमें एक गुहा है जैसा कि चित्र (ए) में दिखाया गया है, को एक चार्ज दिया जाता है Q. दिखाएँ कि पूरा चार्ज कंडक्टर की बाहरी सतह पर दिखाई देना चाहिए।
(बी)चार्ज q के साथ एक अन्य कंडक्टर बी को ए से अछूता रखते हुए गुहा में डाला जाता है। दिखाएँ कि ए की बाहरी सतह पर कुल चार्ज क्यू + क्यू है [चित्र (बी)]।
(सी) एक संवेदनशील उपकरण को अपने पर्यावरण में मजबूत इलेक्ट्रोस्टैटिक क्षेत्रों से संरक्षित किया जाना है। एक संभावित तरीका सुझाएं।
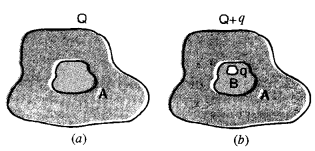
उत्तर:
एक गाऊसी सतह चुनें जो पूरी तरह से कंडक्टर के अंदर हो लेकिन कंडक्टर की सतह के बहुत करीब हो।
(ए) कंडक्टर के अंदर कोई विद्युत क्षेत्र नहीं है इसलिए गाऊसी सतह के माध्यम से विद्युत प्रवाह शून्य है या दूसरे शब्दों में, गाऊसी सतह के अंदर शुद्ध चार्ज शून्य है। तब यह कहा जा सकता है कि आवेश गाऊसी सतह के बाहर स्थित है e. कंडक्टर की बाहरी सतह पर।
(बी)कैविटी के अंदर चार्ज q, कैविटी के अंदरूनी हिस्से पर चार्ज -q को प्रेरित करेगा और इस तरह बाहरी सतह पर +q दिखाई देगा। अत: कुल आवेश (q+Q) होगा।
(सी) उपकरण को धातु के खोल में संलग्न किया जाना चाहिए ताकि इलेक्ट्रोस्टैटिक क्षेत्र का प्रभाव रद्द हो जाए।
प्रश्न 29.
एक खोखले आवेशित चालक के पृष्ठ में एक छोटा सा छेद होता है। दिखाएँ कि छेद में विद्युत क्षेत्र है (σ/2ε 0 )एन^, कहां एन^बाहरी सामान्य दिशा में इकाई वेक्टर है, और छेद के पास सतह चार्ज घनत्व है।
उत्तर:
मान लीजिए कि कंडक्टर के छोटे से छेद को भरा हुआ माना जाता है। कंडक्टर के अंदर क्षेत्र शून्य है, जबकि इसके बाहर द्वारा दिया गया है
![]()
यह क्षेत्र वास्तव में
(1) क्षेत्र (ई 1 ) प्लग होल के कारण और
(2) फ़ील्ड ई 2 शेष चार्ज कंडक्टर के कारण है। कंडक्टर के अंदर, ये क्षेत्र बराबर लेकिन विपरीत होते हैं, जबकि बाहर ये बिल्कुल समान होते हैं। अर्थात
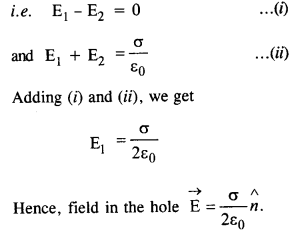
प्रश्न 30.
गॉस के नियम का उपयोग किए बिना एकसमान रैखिक आवेश घनत्व X के लंबे पतले तार के कारण विद्युत क्षेत्र का सूत्र प्राप्त करें।
[संकेत। कूलम्ब के नियम का सीधे प्रयोग करें और आवश्यक समाकलन का मूल्यांकन करें।]
उत्तर:
X-अक्ष के अनुदिश एकसमान रैखिक आवेश घनत्व X के एक लंबे पतले तार पर विचार करें। मान लीजिए कि P, y-अक्ष पर स्थित एक बिंदु है


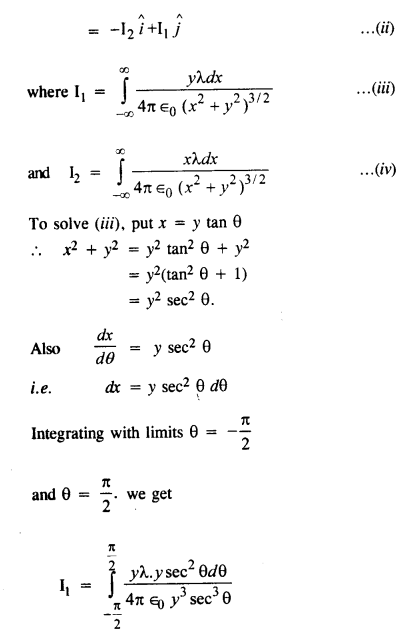
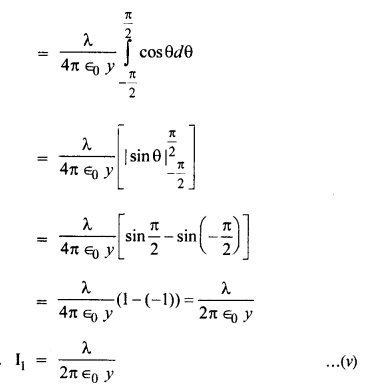

प्रश्न 31।
अब यह माना जाता है कि प्रोटॉन और न्यूट्रॉन (जो साधारण पदार्थ के नाभिक का निर्माण करते हैं) स्वयं क्वार्क नामक अधिक प्राथमिक इकाइयों से निर्मित होते हैं। एक प्रोटॉन और एक न्यूट्रॉन में प्रत्येक में तीन क्वार्क होते हैं। दो प्रकार के क्वार्क, तथाकथित ‘अप’ क्वार्क (यू द्वारा निरूपित) चार्ज + (2/3) ई, और ‘डाउन’ क्वार्क (डी द्वारा दर्शाया गया) चार्ज
(-l/3)e, इलेक्ट्रॉनों के साथ मिलकर साधारण पदार्थ का निर्माण करते हैं। (अन्य प्रकार के क्वार्क भी पाए गए हैं जो पदार्थ की विभिन्न असामान्य किस्मों को जन्म देते हैं।) एक प्रोटॉन और न्यूट्रॉन की संभावित क्वार्क संरचना का सुझाव दें ।)
उत्तर:

प्रश्न 32.
(a) एक मनमाना स्थिरवैद्युत क्षेत्र विन्यास पर विचार कीजिए। एक छोटा परीक्षण आवेश विन्यास के शून्य बिंदु (अर्थात, जहां E = 0) पर रखा जाता है। दिखाएँ कि परीक्षण आवेश का संतुलन आवश्यक रूप से अस्थिर है।
(बी) एक ही परिमाण के दो शुल्कों के सरल विन्यास के लिए इस परिणाम को सत्यापित करें और एक निश्चित दूरी को अलग रखें।
उत्तर:
(ए) परिणाम को साबित करने के लिए, मान लें कि शून्य बिंदु पर रखा गया परीक्षण चार्ज स्थिर संतुलन में है। यदि ऐसा है, तो शून्य बिंदु से थोड़ा दूर विस्थापित होने पर, परीक्षण आवेश अपनी स्थिति में वापस आ जाना चाहिए। इसका तात्पर्य है कि यदि परीक्षण आवेश के चारों ओर एक बंद सतह खींची जाती है, तो विद्युत का शुद्ध आवक प्रवाह होगा इसकी सतह के माध्यम से क्षेत्र। गॉस के नियम के अनुसार, इसकी सतह से कोई विद्युत प्रवाह नहीं हो सकता क्योंकि इसमें कोई आवेश नहीं होता है। इसलिए हमारी धारणा गलत है और परीक्षण
(बी) समान परिमाण और चिन्ह के दो आवेशों के विन्यास के लिए, शून्य बिंदु दो आवेशों को मिलाने वाली रेखा का मध्य बिंदु है। यदि परीक्षण आवेश रेखा के साथ शून्य बिंदु से थोड़ा विस्थापित हो जाता है, तो यह दिन में आने वाले पुनर्स्थापन बल के कारण वापस आ जाएगा। लेकिन अगर चार्ज को नल-पॉइंट से सामान्य के साथ लाइन में थोड़ा विस्थापित किया जाता है, तो यह वापस नहीं आएगा। ऐसा इसलिए है क्योंकि दो आवेशों के विन्यास के कारण परिणामी बल इसे शून्य बिंदु से दूर ले जाएगा। परीक्षण आवेश के स्थिर संतुलन में होने के लिए, जब यह किसी भी दिशा में विस्थापित होता है, तो पुनर्स्थापना बल को खेलना चाहिए। इसलिए परीक्षण आवेश स्थिर संतुलन में नहीं हो सकता है।
प्रश्न 33.
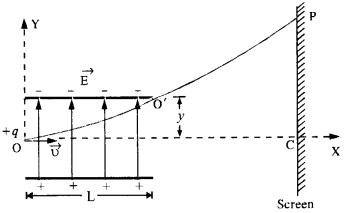
द्रव्यमान m और आवेश (-q) का एक कण प्रारंभ में x-अक्ष के अनुदिश गति σ x के साथ गतिमान दो आवेशित प्लेटों के बीच के क्षेत्र में प्रवेश करता है(जैसे आकृति में कण 1)। प्लेट की लंबाई L और एक समान है। प्लेटों के बीच विद्युत क्षेत्र E बना रहता है। दिखाएँ कि प्लेट के दूर किनारे पर कण का ऊर्ध्वाधर विक्षेपण qEL 2 /(2m x 2 ) है।
इस गति की तुलना धारा 4.10 में चर्चा किए गए गुरुत्वाकर्षण क्षेत्र में प्रक्षेप्य की गति से करें। भौतिकी की ग्यारहवीं कक्षा की पाठ्यपुस्तक।
उत्तर:
एक समान विद्युत क्षेत्र पर विचार करेंइ→दो विपरीत आवेशित समानांतर प्लेटों के बीच स्थापित (चित्र)। मान लीजिए कि एक धनावेशित कण जिसका आवेश +q और द्रव्यमान m है, विद्युत क्षेत्र E के क्षेत्र में O पर वेग E के साथ X-दिशा में प्रवेश करता है।
चरण 1.
विद्युत क्षेत्र E के कारण आवेश +q पर कार्य करने वाला बल किसके द्वारा दिया जाता है?
एफ→ =क्यू इ→
बल की दिशा की दिशा में है
इ→और इसलिए आवेशित कण तदनुसार विक्षेपित हो जाता है।
आवेशित कण में उत्पन्न त्वरण किसके द्वारा दिया जाता है
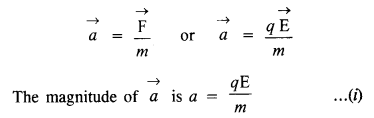
चरण 2.
आवेशित कण E की दिशा में गति करेगा। जैसे ही कण विद्युत क्षेत्र के क्षेत्र को छोड़ता है, यह गति की जड़ता के कारण यात्रा करता है और बिंदु P पर स्क्रीन से टकराता है। मान लीजिए कि आवेशित कण द्वारा लंबाई L के विद्युत क्षेत्र के क्षेत्र को पार करने में लिया गया समय है। माना y कण द्वारा y-दिशा (यानी विद्युत क्षेत्र की दिशा) के साथ तय की गई दूरी हो। गति के एक मानक समीकरण का उपयोग करते हुए,
S = ut +122 बजे ।
क्षैतिज गति के लिए। एस = एल, यू = υ एक्स और ए = 0।
(∴ x-दिशा के साथ कण पर कोई बल नहीं लगता है)
समीकरण (ii) से, हमारे पास

समीकरण (i) एक परवलय का समीकरण है।
इसलिए एक समान विद्युत क्षेत्र में गतिमान आवेशित कण परवलयिक पथ का अनुसरण करता है।
प्रश्न 34.
मान लीजिए कि क्यू 1.33 में कण एक इलेक्ट्रॉन वेग के साथ पेश किया है
υ एक्स = 2.0 x 10 6 एमएस -1 । यदि 0.5 सेमी से अलग की गई प्लेटों के बीच E 9.1 x 10 2 N/C है,
तो इलेक्ट्रॉन ऊपरी प्लेट से कहाँ टकराएगा? ( |e| = 1.6 x 10 -19 C, m e = 9.1 x 10- 31 किग्रा।)
उत्तर:
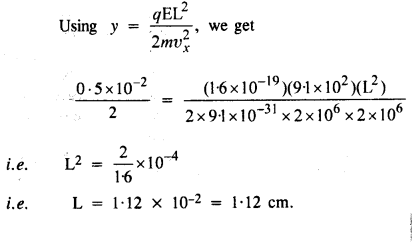
हम उम्मीद करते हैं कि एनसीईआरटी सोलूशन्स क्लास 12 भौतिकी चैप्टर 1 विद्युत आवेश और क्षेत्र आपके लिए मददगार साबित होंगे। यदि आपके पास एनसीईआरटी सोलूशन्स क्लास 12 भौतिकी चैप्टर 1 इलेक्ट्रिक चार्ज और फील्ड्स के बारे में कोई प्रश्न हैं, तो नीचे कमेंट करें और हम आपसे जल्द से जल्द संपर्क करेंगे।


