कक्षा 12 भौतिकी अध्याय 2 इलेक्ट्रोस्टैटिक क्षमता और क्षमता के लिए एनसीईआरटी समाधान

एनसीईआरटी सॉल्यूशंस फॉर क्लास 12 फिजिक्स चैप्टर 2 इलेक्ट्रोस्टैटिक पोटेंशियल एंड कैपेसिटेंस क्लास 12 फिजिक्स के एनसीईआरटी सॉल्यूशंस का हिस्सा हैं । यहां हमने दिया है। कक्षा 12 भौतिकी अध्याय 2 इलेक्ट्रोस्टैटिक क्षमता और क्षमता के लिए एनसीईआरटी समाधान

NCERT Solutions For Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance

तख़्ता	सीबीएसई
पाठयपुस्तक	NCERT
कक्षा	कक्षा 12
विषय	भौतिक विज्ञान
अध्याय	अध्याय दो
अध्याय का नाम	इलेक्ट्रोस्टैटिक क्षमता और समाई
हल किए गए प्रश्नों की संख्या	37
श्रेणी	NCERT Solutions

प्रश्न 1.
दो आवेश 5 x 10^-8C और -3 x 10^-8C 16 सेमी की दूरी पर स्थित हैं। दो आवेशों को मिलाने वाली रेखा पर किस बिंदु पर विद्युत विभव शून्य है? अनंत पर विभव को शून्य मान लें। उत्तर। मान लीजिए 0 पर विभव शून्य है, तो
उत्तर:
मान लीजिए 0 पर विभव शून्य है, फिर v_A+ V_B= 0, जहाँ V_Aआवेश q_{A के}कारण विद्युत विभव हैऔर V_Bआवेश q के कारण विद्युत विभव है_बी.

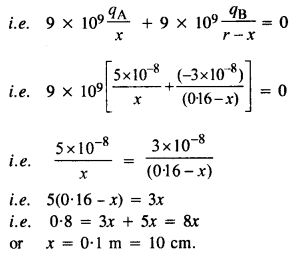
प्रश्न 2.
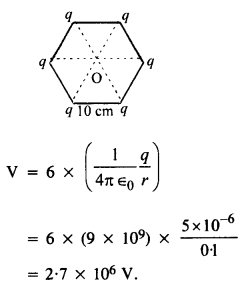
10 सेमी भुजा वाले एक नियमित षट्भुज के प्रत्येक शीर्ष पर 5μC आवेश है। षट्भुज के केंद्र में क्षमता की गणना करें।
उत्तर:
O पर कुल विभव किसके द्वारा दिया जाता है,

प्रश्न 3.
दो आवेश 2μC और -2μC, 6 सेमी की दूरी पर स्थित बिंदुओं A और B पर रखे गए हैं।
(ए) सिस्टम की एक समविभव सतह की पहचान करें। % मध्य-बिंदु से प्रत्येक पर विद्युत क्षेत्र की दिशा क्या है। इस तल पर, हर जगह क्षमता शून्य है।
(बी) विद्युत क्षेत्र की दिशा सकारात्मक से नकारात्मक चार्ज यानी ए से बी तक है, जो वास्तव में समविभव तल के लंबवत है।
उत्तर:
(ए) एक सतह जिसमें एक भूमध्य रेखा और एक लंबवत रेखा होती है।
(बी) – ve चार्ज की तरफ, अक्ष के समानांतर।

प्रश्न 4.
12 सेमी त्रिज्या वाले एक गोलाकार चालक का आवेश 1.6 x 10^-7C है, जो इसकी सतह पर समान रूप से वितरित है। विद्युत क्षेत्र
(a) गोले के अंदर
(b) गोले के ठीक बाहर
(c)गोलेके केंद्र से 18 सेमी की दूरी पर क्या है?
उत्तर:
(ए)एक कंडक्टर के अंदर, विद्युत क्षेत्र शून्य है क्योंकि चार्ज एक कंडक्टर की सतह पर रहता है।
(बी)गोले के ठीक बाहर विद्युत क्षेत्र

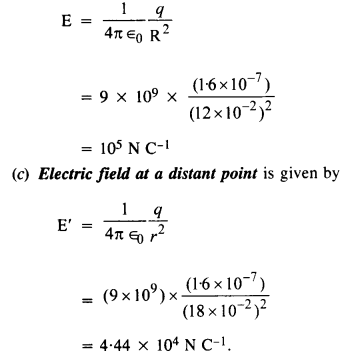
प्रश्न 5 द्वारा दिया गया है
। प्लेटों के बीच हवा के साथ समानांतर प्लेट कैपेसिटर की क्षमता 8 पीएफ
(1 पीएफ = 10^{-12 है)}एफ.) यदि प्लेटों के बीच की दूरी को आधा कर दिया जाए और उनके बीच का स्थान ढांकता हुआ स्थिरांक 6 के पदार्थ से भर दिया जाए तो धारिता क्या होगी?
उत्तर:

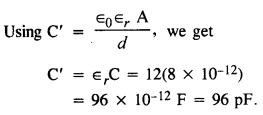
प्रश्न 6.
तीन कैपेसिटर प्रत्येक की धारिता 9pF श्रृंखला में जुड़े हुए हैं।
(ए) संयोजन की कुल क्षमता क्या है?
(बी) यदि संयोजन 120 वी आपूर्ति से जुड़ा हुआ है तो प्रत्येक संधारित्र में संभावित अंतर क्या है?
उत्तर:

प्रश्न 7.
दो पीएफ, 3 पीएफ और 4 पीएफ की धारिता के तीन कैपेसिटर समानांतर में जुड़े हुए हैं।
(ए) संयोजन की कुल क्षमता क्या है?
(बी) प्रत्येक संधारित्र पर चार्ज निर्धारित करें यदि संयोजन 100 वी आपूर्ति से जुड़ा हुआ है।
उत्तर:
(ए)कुल समाई
= सी₁+ सी₂+ सी₃
= 2 + 3+ 4 = 9pF।
(बी)सी = . का उपयोग करनाक्यूवीहमें q = CV
q _x = C ₁ V = 2 x 10- ¹² x 100
= 2 x 10- ¹⁰ C = 200 pC
q ₂ = c ₂ V
= 3 x 10 ^-12  x 100
= 3 x 10- ^{10 मिलता है।} सी = ३०० पीसी
क्यू _३ = सी _३ वी
= ४ x १०- ^१२ x १००
= ४ x १०- ^१० सी = ४०० पीसी

प्रश्न 8.
प्लेटों के बीच हवा के साथ एक समानांतर प्लेट संधारित्र अलावा, प्रत्येक प्लेट का क्षेत्रफल है
6 x 10^-3में²और प्लेटों के बीच की दूरी 3 मिमी है। संधारित्र की धारिता की गणना कीजिए। यदि इस संधारित्र को 100 वोल्ट की आपूर्ति से जोड़ा जाए, तो संधारित्र की प्रत्येक प्लेट पर कितना आवेश होगा?
उत्तर:

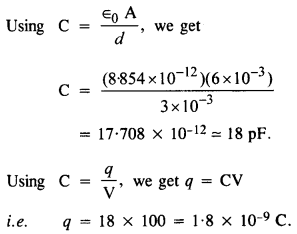
प्रश्न 9.
बताएं कि क्या होगा यदि Q. 2.8 में दिए गए संधारित्र में, प्लेटों के बीच एक 3 मिमी मोटी अभ्रक शीट (डाइलेक्ट्रिक स्थिरांक = 6) डाली जाए,
(a) जबकि वोल्टेज की आपूर्ति बनी रहे।
(बी) आपूर्ति बंद होने के बाद।
उत्तर:

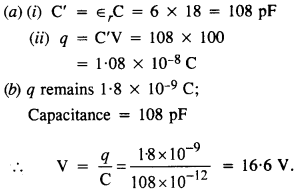
प्रश्न 10.
एक 12 pF संधारित्र को 50 V की बैटरी से जोड़ा जाता है। संधारित्र में कितनी स्थिरवैद्युत ऊर्जा संचित होती है?
उत्तर:
ई =12सीवी ² =12x १२ x १०- ^१२ x ५० x ५० = १.५ २ २ x १०- ^८ जे।

प्रश्न 11.
एक 600 pF संधारित्र को 200 V की आपूर्ति द्वारा आवेशित किया जाता है। फिर इसे डाई आपूर्ति से काट दिया जाता है और एक अन्य अपरिवर्तित 600 pF संधारित्र से जोड़ा जाता है। प्रक्रिया में कितनी इलेक्ट्रोस्टैटिक ऊर्जा खो जाती है?
उत्तर।
यहाँ, C₁= 600pF = 6 x 10^-10F, C₂=
6 x 10-¹⁰F, V₁= 200V, V₂= 0

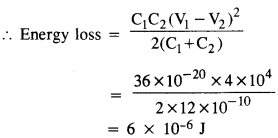
प्रश्न 12.
मूल बिंदु पर 8 mC का आवेश स्थित है। एक बिंदु P(0, 0, 3 सेमी) से एक बिंदु Q (0, 4 सेमी, 0) तक एक बिंदु R(0, 6) के माध्यमसे -2 x 10^-9Cका एक छोटा आवेश लेने में किए गए कार्य की गणना करें।
सेमी, 9 सेमी.)
उत्तर:
किसी आवेश पर स्थिरवैद्युत बल द्वारा किया गया कार्य आवेश द्वारा अनुसरित पथ से स्वतंत्र होता है। यह केवल आवेश की प्रारंभिक और अंतिम स्थिति पर निर्भर करता है।

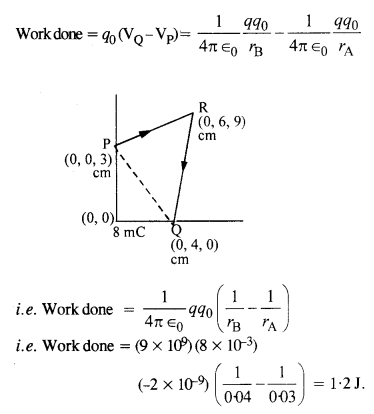
प्रश्न 13.
भुजा b वाले घन के प्रत्येक शीर्ष पर q आवेश है। घन के केंद्र में इस आवेश सरणी के कारण संभावित और विद्युत क्षेत्र का निर्धारण करें।
उत्तर:
(१) शीर्ष से घन के केंद्र की दूरी घन के विकर्ण की आधी है

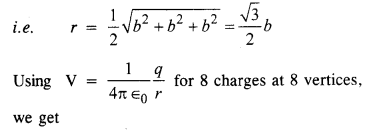
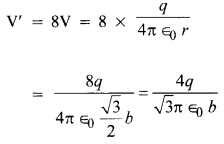
(२) सममिति से यह स्पष्ट है कि घन के केंद्र में विद्युत क्षेत्र शून्य है।

प्रश्न 14.
1.5 μc और 2.5 μc आवेश वाले दो छोटे गोले 30 cm की दूरी पर स्थित हैं। संभावित और विद्युत क्षेत्र का पता लगाएं:
(ए) दो आवेशों को मिलाने वाली रेखा के मध्य बिंदु पर,
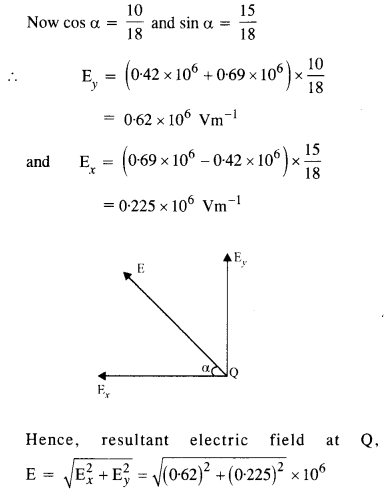
(बी) इस मध्य-बिंदु से एक बिंदु पर 10 सेमी की रेखा के सामान्य और मध्य बिंदु से गुजरते हुए।
उत्तर:

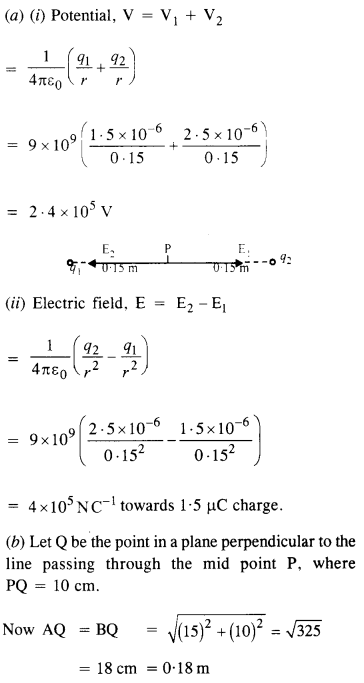
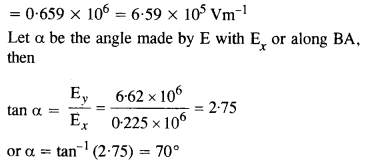
प्रश्न 15.
आंतरिक त्रिज्या r_lऔर बाहरी त्रिज्या r_{2 के}एक गोलाकार संवाहक खोलमें एक चार्ज Q होता है।
(a) एक चार्ज q कोश के केंद्र में रखा जाता है। खोल की आंतरिक और बाहरी सतहों पर सतह आवेश घनत्व क्या है?
(बी) क्या कोश गोलाकार न होने पर भी एक गुहा (बिना आवेश के) के अंदर विद्युत क्षेत्र शून्य है, लेकिन उसका कोई अनियमित आकार है? समझाना।
उत्तर:
(ए)चार्ज क्यू बाहरी सतह पर दिखाई देता है।

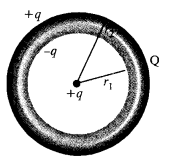
जब आवेश q को केंद्र में रखा जाता है, तो यह – q आवेश को आंतरिक सतह पर और +q बाहरी सतह पर प्रेरित करता है।
.’. आंतरिक सतह का चार्ज घनत्व,

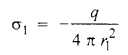
और बाहरी सतह का चार्ज घनत्व,

एक अनियमित आकार की गुहा पर विचार करें जिसके अंदर नेट चार्ज शून्य हो। एक बंद लूप को आंशिक रूप से अंदर और बाकी को गुहा के बाहर होने दें। कंडक्टर के अंदर का क्षेत्र शून्य है, इसलिए बंद लूप में परीक्षण चार्ज करने के लिए क्षेत्र द्वारा कुछ काम किया जाता है, लेकिन यह इलेक्ट्रोस्टैटिक क्षेत्र के प्रावधानों के खिलाफ है क्योंकि गॉस के नियम के अनुसार, गॉसियन सतह के अंदर शुद्ध चार्ज शून्य होना चाहिए। इस प्रकार, गुहा के अंदर क्षेत्र रेखाएँ नहीं हो सकती हैं, चाहे उसका आकार कुछ भी हो।

प्रश्न 16.
(ए) दिखाएँ कि इलेक्ट्रोस्टैटिक क्षेत्र के सामान्य घटक में एक चार्ज सतह के एक तरफ से दूसरी तरफ एक असंततता होती है,

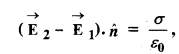
जहां सेदिया जाता हैएन^एक बिंदु पर सतह के लिए सामान्य एक इकाई वेक्टर है और उस बिंदु पर सतह चार्ज घनत्व है। (h की दिशा 1 भुजा से 2 भुजा की ओर है।) अतः दर्शाइए कि चालक के ठीक बाहर विद्युत क्षेत्र . हैएन^/ε ₀
(बी) दिखाएँ कि इलेक्ट्रोस्टैटिक क्षेत्र का स्पर्शरेखा घटक एक चार्ज सतह के एक तरफ से दूसरी तरफ निरंतर है। [संकेत। (ए) के लिए गॉस के नियम का प्रयोग करें। के लिए, (बी) इस तथ्य का उपयोग करें कि बंद लूप पर इलेक्ट्रोस्टैटिक क्षेत्र द्वारा किया गया कार्य शून्य है।]
उत्तर:
चार्ज घनत्व वाले चार्ज शीट पर विचार करें ए। ई शीट के दोनों ओर, शीट के तल के लंबवत, शीट से समान दूरी पर सभी बिंदुओं पर समान परिमाण है।
शीट के बाईं ओर विद्युत क्षेत्र की तीव्रता,

प्लेट के लिए स्पर्शरेखा विद्युत क्षेत्र निरंतर है।

Question 17.
रैखिक आवेशित घनत्व A का एक लंबा आवेशित सिलेंडर एक खोखले सह-अक्षीय संवाहक सिलेंडर से घिरा हुआ है। दो सिलेंडरों के बीच की जगह में विद्युत क्षेत्र क्या है?
उत्तर:
एक बेलन P में रैखिक आवेश घनत्व, , लंबाई l, और त्रिज्या r_{1 है}
। बेलन P, q = XL पर आवेश लंबाई / और त्रिज्या r_{2 का}एक खोखला सह-अक्षीय संवाहक सिलेंडरसिलेंडर P को घेरता है। सिलेंडर पर चार्ज क्यू = – क्यू।

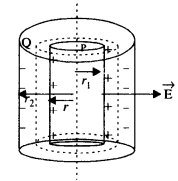
त्रिज्या r और लंबाई l के बेलन के रूप में एक गाऊसी सतह पर विचार करें। गाऊसी सतह की घुमावदार सतह के माध्यम से विद्युत प्रवाह,

प्रश्न 18.
हाइड्रोजन परमाणु में, इलेक्ट्रॉन और प्रोटॉन लगभग 0.53 की दूरी पर बंधे होते हैं:
(ए) ईवी में सिस्टम की संभावित ऊर्जा का अनुमान लगाएं, इलेक्ट्रॉन के अनंत अलगाव पर संभावित ऊर्जा का शून्य लेते हुए प्रोटॉन।
(बी) इलेक्ट्रॉन को मुक्त करने के लिए आवश्यक न्यूनतम कार्य क्या है, यह देखते हुए कि कक्षा में इसकी गतिज ऊर्जा (ए) में प्राप्त संभावित ऊर्जा का आधा परिमाण है?
(सी) उपरोक्त (ए) और (बी) के उत्तर क्या हैं यदि संभावित ऊर्जा का शून्य 1.06 ए अलगाव पर लिया जाता है?
उत्तर:

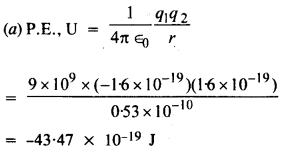
प्रश्न 19.
अगर एक एच के दो इलेक्ट्रॉनों की एक₂अणु निकाल दिया जाता है, हम एक हाइड्रोजन आणविक आयन एच मिल⁺₂। एच⁺₂की जमीनी अवस्था में, दो प्रोटॉन लगभग 1.5 से अलग होते हैं, और इलेक्ट्रॉन प्रत्येक प्रोटॉन से लगभग होता है। सिस्टम की संभावित ऊर्जा का निर्धारण करें। शून्य स्थितिज ऊर्जा के अपने चयन को निर्दिष्ट करें।
उत्तर:

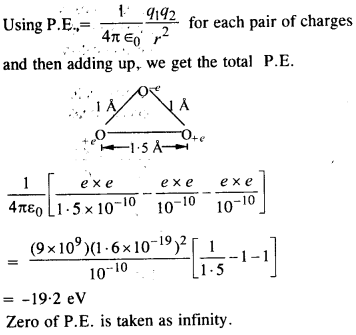
प्रश्न 20.
त्रिज्या a और b के दो आवेशित चालक गोले एक दूसरे से एक तार द्वारा जुड़े हुए हैं। दो गोले की सतहों पर विद्युत क्षेत्र का अनुपात क्या है? प्राप्त परिणाम का उपयोग यह समझाने के लिए करें कि किसी चालक के नुकीले और नुकीले सिरों पर आवेश घनत्व उसके समतल भागों की तुलना में अधिक क्यों होता है।
उत्तर:
एक तार से जुड़े त्रिज्या a और b के दो आवेशित चालक गोले समान विभव तक पहुंचेंगे।

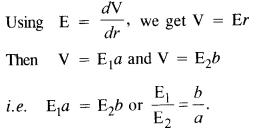
स्पष्ट रूप से, नुकीली सतह के लिए विद्युत आवेश घनत्व अधिक होगा क्योंकि एक सपाट सतह को बड़े त्रिज्या के गोलाकार सतह और एक नुकीले हिस्से को छोटे त्रिज्या के गोलाकार सतह के बराबर किया जा सकता है।

प्रश्न 21.
दो आवेश -q और + q क्रमशः बिंदुओं (0, 0, -a) और (0, 0, a) पर स्थित हैं।
(ए) बिंदुओं (0, 0, जेड) और (एक्स, वाई, 0) पर इलेक्ट्रोस्टैटिक क्षमता क्या है?
(बी) मूल से एक बिंदु की दूरी r पर क्षमता की निर्भरता प्राप्त करें जब r/a>> 1.
(c) बिंदु से एक छोटे परीक्षण चार्ज को स्थानांतरित करने में कितना काम किया जाता है (5, 0, 0) से (-7, 0, 0) x-अक्ष के अनुदिश? यदि समान बिंदुओं के बीच परीक्षण आवेश का पथ x-अक्ष के अनुदिश न हो तो क्या उत्तर बदल जाता है?
उत्तर:

बिंदु (x, y, 0) Z-अक्ष के लंबवत है, इसलिए (x, y, 0) पर विभव शून्य है।
(बी)पी को विद्युत द्विध्रुव के केंद्र (ओ) से दूरी r पर अवलोकन बिंदु मानें।
OP को द्विध्रुव आघूर्ण के साथ 0 कोण बनाने दें पी→
और r _1, r ₂ क्रमशः – q आवेश और + q आवेश से बिंदु P की दूरी हो। P पर विभव – q आवेश के कारण,



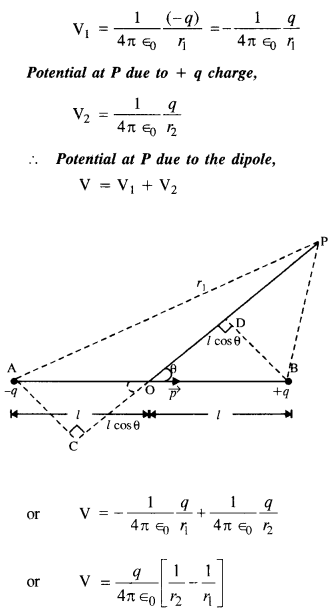
उत्तर नहीं बदलता है, क्योंकि इलेक्ट्रोस्टैटिक्स में, किया गया कार्य वास्तविक पथ पर निर्भर नहीं करता है, यह केवल प्रारंभिक और अंतिम स्थिति पर निर्भर करता है।

प्रश्न 22.
आकृति एक आवेश सरणी को दर्शाती है जिसे विद्युत चतुर्भुज के रूप में जाना जाता है। चतुर्भुज की धुरी पर एक बिंदु के लिए, r/a>> l के लिए r पर क्षमता की निर्भरता प्राप्त करें, और एक विद्युत द्विध्रुव, और एक विद्युत मोनोपोल
(अर्थात, एक एकल आवेश) केकारण अपने परिणामों के साथ इसके विपरीत करें।

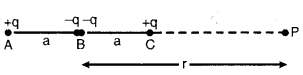
उत्तर :

(2) विद्युत द्विध्रुव के कारण विभव 1/r²प्रकार का होता है।
(३) एक विद्युत मोनोपोल के कारण, क्षमता १/r प्रकार की होती है।

प्रश्न 23.
एक विद्युत तकनीशियन को 1 kV के विभवान्तर के परिपथ में 2 μF की धारिता की आवश्यकता होती है। उसके लिए बड़ी संख्या में 1 μF कैपेसिटर उपलब्ध हैं, जिनमें से प्रत्येक 400 V से अधिक के संभावित अंतर का सामना कर सकता है। एक संभावित व्यवस्था का सुझाव दें जिसमें कैपेसिटर की न्यूनतम संख्या की आवश्यकता हो।
उत्तर:
मान लीजिए कि N संधारित्रों का उपयोग m पंक्तियों में किया जाता है जब प्रत्येक पंक्ति में n संधारित्र अर्थात N = mn
श्रेणी

प्रश्न 24 में हो।
2 एफ समानांतर प्लेट कैपेसिटर की प्लेटों का क्षेत्रफल क्या है, यह देखते हुए कि प्लेटों के बीच की दूरी 0.5 सेमी है? (आप अपने उत्तर से महसूस करेंगे कि साधारण कैपेसिटर μF या उससे कम की सीमा में क्यों होते हैं। हालांकि, इलेक्ट्रोलाइटिक कैपेसिटर में कंडक्टरों के बीच बहुत कम दूरी के कारण बहुत अधिक समाई ((0.1 F) होती है।)
उत्तर:

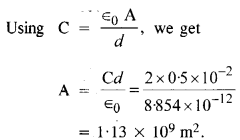
प्रश्न 25.
चित्र में नेटवर्क की तुल्य धारिता ज्ञात कीजिए। 300 वी आपूर्ति के लिए, प्रत्येक संधारित्र में चार्ज और वोल्टेज निर्धारित करें। (सीबीएसई 2008)

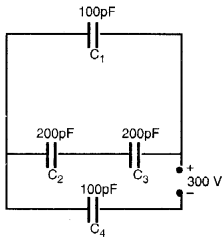
उत्तर:
समकक्ष सर्किट नीचे दिखाया गया है:

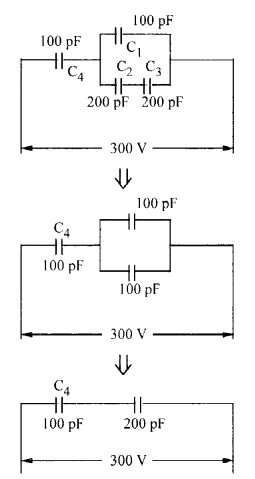
सी_{4 में}संभावित अंतर2:1
यानी 200 वीके अनुपात में है
। सी₄= सी₄वी₄
= 100 x 200 x 10^-12= 2 x 10^-8सी पर चार्ज
सी₁= 100 वी
परसंभावित अंतरसी₁ = सी₁एक्स वी₁
= 100 x 100 x 10-¹²= 1 x 10^-8सी ₂ और सी ₃ में
संभावित अंतर 50 वी प्रत्येक है सी ₂ या सी ₃ पर चार्ज = सी ₂ वी ₂ = 200 x 50 x 10 ^-12 = 10- ⁸ सी।

प्रश्न 26.
एक समान्तर प्लेट संधारित्र की प्लेटों का क्षेत्रफल 90 सेमी^{2 है}और वे 2.5 मिमी से अलग हैं। संधारित्र को 400 वोल्ट की आपूर्ति से जोड़कर चार्ज किया जाता है।
(ए) संधारित्र द्वारा कितनी इलेक्ट्रोस्टैटिक ऊर्जा संग्रहीत की जाती है?
(बी) इस ऊर्जा को प्लेटों के बीच इलेक्ट्रोस्टैटिक क्षेत्र में संग्रहीत के रूप में देखें, और प्रति यूनिट मात्रा में ऊर्जा प्राप्त करें इसलिए प्लेटों के बीच यू और विद्युत क्षेत्र ई के परिमाण के बीच संबंध पर पहुंचें।
उत्तर:

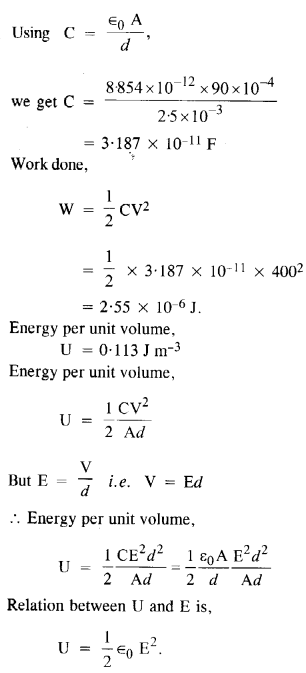
प्रश्न 27.
एक 4 μF संधारित्र को 200 V की आपूर्ति द्वारा चार्ज किया जाता है। फिर इसे आपूर्ति से काट दिया जाता है और एक अन्य अपरिवर्तित 2 μF संधारित्र से जोड़ा जाता है। ऊष्मा और विद्युतचुंबकीय विकिरण के रूप में पहले संधारित्र की विद्युत स्थैतिक ऊर्जा कितनी नष्ट हो जाती है?
उत्तर:

प्रश्न 28. दर्शाइए
कि समानांतर प्लेट संधारित्र की प्रत्येक प्लेट पर लगने वाले बल का परिमाण (1/2) QE है, जहाँ Q संधारित्र पर आवेश है और E प्लेटों के बीच विद्युत क्षेत्र का परिमाण है। कारक की उत्पत्ति (1/2) की व्याख्या करें।
उत्तर:
मान लीजिए कि F संधारित्र की प्रत्येक प्लेट पर लगने वाला बल है। यदि संधारित्र की प्लेटों के बीच की दूरी dx बढ़ा दी जाती है, तो किया गया कार्य = F dx। किया गया यह कार्य संधारित्र की स्थितिज ऊर्जा के रूप में संचित हो जाता है। संधारित्र के आयतन में वृद्धि = A dx

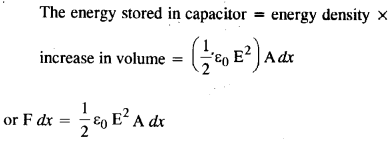
प्रश्न 29.
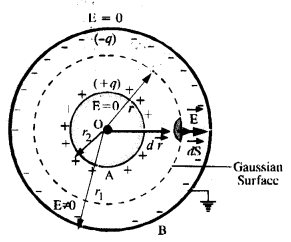
एक गोलाकार संधारित्र में दो संकेंद्रित गोलाकार कंडक्टर होते हैं जो उपयुक्त इन्सुलेट समर्थन द्वारा स्थिति में होते हैं (चित्र।) दिखाएँ कि गोलाकार संधारित्र की धारिता दी जाती है

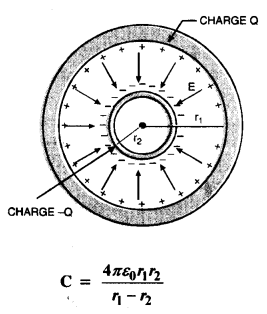
जहाँ r_xऔर r₂क्रमशः बाहरी और आंतरिक क्षेत्रों की त्रिज्याएँ हैं। .
उत्तर:
इसमें दो संकेंद्रित गोलाकार गोले A और B हैं जिनकी त्रिज्याएँ a और b क्रमशः आवेश +q और आवेश -q हैं। (बाहरी गोला जमी हुई है)

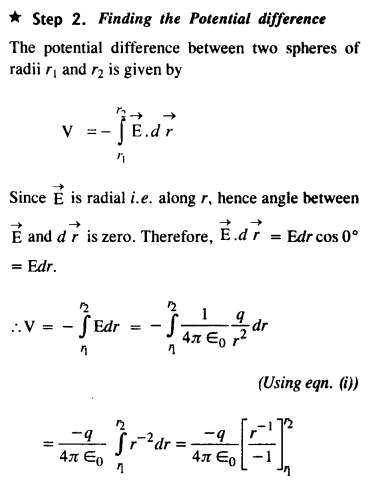
Question 30.
एक गोलाकार संधारित्र में त्रिज्या 12 सेमी का एक आंतरिक क्षेत्र और त्रिज्या 13 सेमी का बाहरी क्षेत्र होता है। बाहरी गोले को धरती पर रखा गया है और भीतरी गोले को 2.5 pC का आवेश दिया गया है। संकेंद्रित गोले के बीच का स्थान ढांकता हुआ स्थिरांक 32 के तरल से भरा होता है।
(ए) संधारित्र की धारिता निर्धारित करें।
(बी) आंतरिक क्षेत्र की क्षमता क्या है?
(c) इस संधारित्र की धारिता की तुलना 12 सेमी त्रिज्या वाले एक पृथक गोले की धारिता से करें। बताएं कि बाद वाला बहुत छोटा क्यों है।
उत्तर:

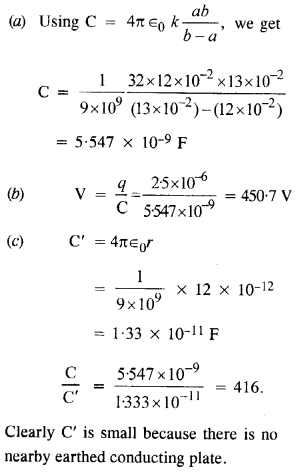
प्रश्न 31.
ध्यान से उत्तर दें:
(ए) चार्ज करने वाले दो बड़े संचालन क्षेत्र क्यू₁और क्यू₂एक दूसरे के करीब लाए जाते हैं। क्या उनके बीच स्थिरवैद्युत बल का परिमाण Q ₁ Q ₂ /4Πε ₀ r ² द्वारा सटीक रूप से दिया गया है , जहां r उनके केंद्रों के बीच की दूरी है?
(बी) यदि कूलम्ब के नियम में 1/r ³ निर्भरता शामिल है (1/r ^{2 के} बजाय ), तो क्या गॉस का नियम अभी भी सत्य होगा?
(सी) एक इलेक्ट्रोस्टैटिक क्षेत्र विन्यास में एक बिंदु पर आराम से एक छोटा परीक्षण चार्ज जारी किया जाता है। क्या यह उस बिंदु से गुजरने वाली क्षेत्र रेखा के अनुदिश यात्रा करेगी?
(d) इलेक्ट्रॉन की पूर्ण वृत्तीय कक्षा में नाभिक के क्षेत्र द्वारा किया जाने वाला कार्य क्या है? क्या होगा यदि कक्षा अण्डाकार है?
(e) हम जानते हैं कि आवेशित चालक के पृष्ठ पर विद्युत क्षेत्र असंतत होता है। क्या वहां विद्युत विभव भी असंतत है?
(च) एकल चालक की धारिता को आप क्या अर्थ देंगे?
(छ) एक संभावित कारण का अनुमान लगाएं कि पानी में अभ्रक (= 6) की तुलना में बहुत अधिक ढांकता हुआ स्थिरांक (= 80) है।
उत्तर:
(ए) नहीं। दिया गया संबंध कूलम्ब का नियम है जो बिंदु आवेशों के लिए सत्य है। वर्तमान मामले में, जैसे-जैसे गोले करीब आते हैं, उन पर आवेश का वितरण असमान हो जाता है।

(बी) नहीं। अंतरिक्ष में सतह क्षेत्र r _{2 के} रूप में बदलता है ताकि क्षेत्र के रूप में भिन्न हो1आर2. अत1आर2 निर्भरता जरूरी है।

(सी) जरूरी नहीं। आवेशित कणों की गति क्षेत्र रेखा के अनुदिश नहीं होनी चाहिए। यह वर्दी क्षेत्र में ऐसा करता है। क्षेत्र त्वरण की दिशा देता है न कि सामान्य रूप से वेग की।

(डी) शून्य। इलेक्ट्रोस्टैटिक क्षेत्र में किसी भी पूर्ण पथ के लिए (आकार कोई फर्क नहीं पड़ता), यह शून्य है।

(ई) नहीं। वहां क्षमता निरंतर है।

(च) एकल कंडक्टर दूसरे कंडक्टर के साथ अनंत पर एक कंडेनसर बना सकता है। इसलिए चार्ज के भंडारण का अर्थ बरकरार रहता है।

(छ) पानी के अणु ध्रुवीय अणु होते हैं।

Question 32.
एक बेलनाकार संधारित्र में 15 सेमी लंबाई और 1.5 सेमी और 1.4 सेमी त्रिज्या के दो समाक्षीय सिलेंडर होते हैं। बाहरी सिलेंडर को अर्थ किया जाता है और आंतरिक सिलेंडर को 3.5 pC का चार्ज दिया जाता है। सिस्टम की क्षमता और आंतरिक सिलेंडर की क्षमता का निर्धारण करें। उपेक्षा अंत प्रभाव, (अर्थात, अंत में क्षेत्र रेखाओं का झुकना)
उत्तर:
एक बेलनाकार संधारित्र की धारिता


प्रश्न 33 द्वारा दी गई है ।
एक समानांतर प्लेट संधारित्र को 1 kV की वोल्टेज रेटिंग के साथ ढांकता हुआ सामग्री का उपयोग करके डिज़ाइन किया जाना है निरंतर 3 और लगभग 10⁷वीएम^{-1 .}की ढांकता हुआ ताकत. (ढांकता हुआ ताकत अधिकतम विद्युत क्षेत्र है जिसे कोई सामग्री बिना ब्रेकडाउन के सहन कर सकती है, अर्थात, आंशिक आयनीकरण के माध्यम से बिजली का संचालन शुरू किए बिना।) सुरक्षा के लिए, हमें यह पसंद करना चाहिए कि क्षेत्र कभी भी अधिक न हो, ढांकता हुआ ताकत का 10%। ५० pF की धारिता रखने के लिए प्लेटों के कितने न्यूनतम क्षेत्रफल की आवश्यकता होती है?
उत्तर:
दिए गए क्षेत्र का 10% अर्थात 10 ⁷ V m ¹ देता है E = 0.1 X 10 ⁷ Vnr ¹

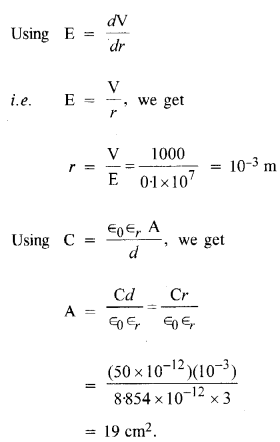
प्रश्न 34. (a) z-दिशा में एक स्थिर विद्युत क्षेत्र, (b) a के
संगत समविभव सतहों का योजनाबद्ध रूप से वर्णन करें वह क्षेत्र जो परिमाण में समान रूप से बढ़ता है लेकिन स्थिर (मान लीजिए, z) दिशा में रहता है,

(सी) मूल पर एक सकारात्मक चार्ज, और
(डी) एक समान ग्रिड जिसमें एक विमान में समान दूरी पर समानांतर चार्ज तार शामिल होते हैं।
उत्तर:
(ए) XY विमान के समानांतर एक विमान।
(बी) एक्सवाई विमान के समानांतर विमान लेकिन विभिन्न निश्चित क्षमता वाले विमान क्षेत्र की तीव्रता में वृद्धि के साथ करीब हो जाएंगे।
(सी) केंद्र के रूप में मूल के साथ केंद्रित क्षेत्र।
(डी) ग्रिड के नजदीक एक समय-निर्भर बदलती आकृति जो धीरे-धीरे प्लानर बन जाती है और ग्रिड से दूर दूरी पर ग्रिड के समानांतर होती है।

प्रश्न 35.
वैन डी ग्रैफ प्रकार के जनरेटर में एक गोलाकार धातु का खोल 15 X 10⁶V इलेक्ट्रोड होना चाहिए। इलेक्ट्रोड के आसपास की गैस की ढांकता हुआ ताकत 5 x 10⁷vm^{-1 है}। गोलाकार कोश की न्यूनतम त्रिज्या कितनी होनी चाहिए? (आप इस अभ्यास से सीखेंगे कि एक बहुत छोटे शेल का उपयोग करके इलेक्ट्रोस्टैटिक जनरेटर का निर्माण क्यों नहीं किया जा सकता है जिसके लिए उच्च क्षमता प्राप्त करने के लिए एक छोटे चार्ज की आवश्यकता होती है।)(सीबीएसई 2008)
उत्तर:
वैन डे ग्रैफ जनरेटर के शेल का न्यूनतम त्रिज्या है संबंध द्वारा दिए गए

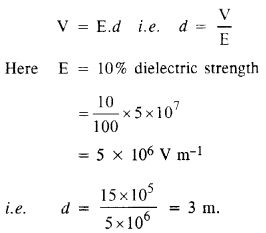
प्रश्न 36.
r त्रिज्या का एक छोटा सा क्षेत्र₁और आवेश q₁ r त्रिज्या का एक गोलाकार खोल में बंद₂और चार्ज क्यू ₂  । दिखाएँ कि यदि q ₁ धनात्मक है, तो आवेश आवश्यक रूप से गोले से खोल में प्रवाहित होगा (जब दोनों एक तार से जुड़े होते हैं) चाहे खोल पर आवेश
q ₂ कोई भी हो ।
उत्तर:
आवेश किसी चालक के बाहरी पृष्ठ पर होता है। अतः आंतरिक गोले पर आवेश चालक तार के माध्यम से खोल की ओर प्रवाहित होगा। इसके अलावा, गॉस के नियम से, गॉसियन सतह के अंदर कोई विद्युत क्षेत्र मौजूद नहीं है, और एक बंद सतह से घिरे चार्ज भी केवल क्षेत्र की ओर योगदान करते हैं। तो इस मामले में q ₂ कोई मायने नहीं रखता। यह सकारात्मक है, एक संभावित अंतर भी सकारात्मक है।

प्रश्न 37.
निम्नलिखित का उत्तर दें:
(ए) वायुमंडल का शीर्ष पृथ्वी की सतह के संबंध में लगभग 400 केवी पर है, जो ऊंचाई के साथ घटने वाले विद्युत क्षेत्र के अनुरूप है। पृथ्वी की सतह के पास, क्षेत्र लगभग 100 Vm^{_1 है}। फिर जब हम अपने घर से बाहर खुले में कदम रखते हैं तो हमें बिजली का झटका क्यों नहीं लगता? (मान लें कि घर एक तारकीय पिंजरा है, इसलिए अंदर कोई खेत नहीं है!)
(बी) एक आदमी एक शाम अपने घर के बाहर दो मीटर ऊंचा इंसुलेटिंग स्लैब लगाता है, जिसके शीर्ष पर 1 मीटर²क्षेत्र की एक बड़ी एल्यूमीनियम शीट होती है। यदि वह अगली सुबह धातु की चादर को छूता है तो क्या उसे बिजली का झटका लगेगा?
(सी) हवा की छोटी चालकता के कारण वायुमंडल में डिस्चार्जिंग करंट को दुनिया भर में औसतन १८०० ए के रूप में जाना जाता है। फिर वायुमंडल अपने आप को नियत समय में पूरी तरह से निर्वहन क्यों नहीं करता है और विद्युत रूप से तटस्थ हो जाता है? दूसरे शब्दों में, क्या वातावरण को आवेशित रखता है?
(घ) तड़ित के दौरान ऊर्जा के कौन से रूप हैं जिनमें वायुमंडल की विद्युत ऊर्जा नष्ट हो जाती है?
[संकेत। पृथ्वी की सतह पर नीचे की दिशा में लगभग 100 Vm ^-1 का विद्युत क्षेत्र है , जो सतह आवेश घनत्व के अनुरूप है = -10 ^-9 C m ^-2. लगभग ५० किमी (जिसके आगे यह अच्छा संवाहक है) तक वायुमंडल की हल्की चालकता के कारण, लगभग ११८०० C प्रति सेकंड समग्र रूप से पृथ्वी में पंप किया जाता है। हालाँकि, पृथ्वी का निर्वहन नहीं होता है क्योंकि पूरे विश्व में लगातार होने वाली गरज और बिजली पृथ्वी पर समान मात्रा में ऋणात्मक आवेश को पंप करती है।]
उत्तर:
(क) हमारा शरीर और जमीन एक समविभव सतह बनाते हैं। जैसे ही हम खुले में कदम रखते हैं, खुली हवा की मूल समविभव सतहें बदल जाती हैं, हमारे सिर और जमीन को समान क्षमता पर रखते हुए।

(बी) हाँ। वातावरण में स्थिर डिस्चार्जिंग करंट धीरे-धीरे एल्युमिनियम शीट को चार्ज करता है और कैपेसिटर की कैपेसिटेंस (शीट, स्लैब और ग्राउंड द्वारा निर्मित) के आधार पर इसके वोल्टेज को एक हद तक बढ़ा देता है।

(सी) पूरे विश्व में गरज और बिजली से वातावरण लगातार चार्ज किया जा रहा है और सामान्य मौसम के क्षेत्रों के माध्यम से छुट्टी दे दी गई है। दो विरोधी धाराएं, औसतन, संतुलन में हैं।

(डी) बिजली में शामिल प्रकाश ऊर्जा; साथ में गड़गड़ाहट में गर्मी और ध्वनि ऊर्जा।

हम उम्मीद करते हैं कि एनसीईआरटी सोलूशन्स क्लास 12 भौतिकी चैप्टर 2 स्थिरवैद्युत विभव एवं धारिता आपके लिए मददगार साबित होंगे। यदि आपके पास एनसीईआरटी सोलूशन्स क्लास 12 भौतिकी चैप्टर 2 इलेक्ट्रोस्टैटिक पोटेंशियल और कैपेसिटेंस के बारे में कोई प्रश्न हैं, तो नीचे एक टिप्पणी करें और हम आपसे जल्द से जल्द संपर्क करेंगे।